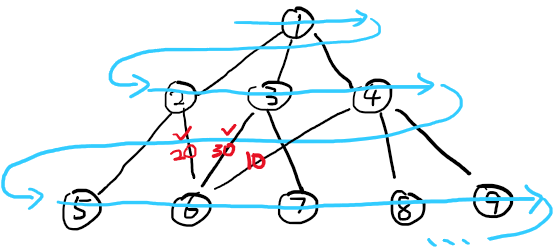
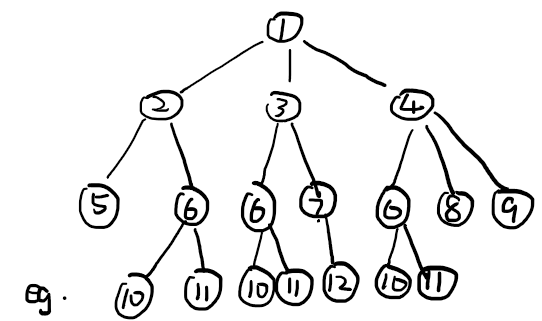
LSD原理:从最低位到最高位,将每个数字放入这一位数对应的桶中,再依次按顺序倒出,即优先度越高的元素(更高位的数),越在后面排序。
LSD代码:(使用了STL,提高输入数据大小、长度的灵活性)
#include <iostream>
#include <vector>
using namespace std;
const int DIGITS = 10;
int max(vector<int>);
int count_digit(int);
int get_digit(int num, int cnt);
int main()
{
vector<int> datas = { 36,5,16,98,1123,1523,1698,5,98,95,47,32,36,48,10,423,455,127,432,123,834,678,176 };
for (int digit = 0; digit < count_digit(max(datas)); digit++)
{
vector<int> t[DIGITS] = {};
for (auto num : datas)
(t + get_digit(num, digit))->push_back(num);
datas.clear();
for (int i = 0; i < DIGITS; i++)
for (auto num : t[i])
datas.push_back(num);
}
for (auto num : datas)
cout << num << ' ';
return 0;
}
int max(vector<int> datas)
{
int max = 0;
for(auto num : datas)
max = num > max ? num : max;
return max;
}
int count_digit(int n)
{
if (n < 10)
return 1;
else
return count_digit(n / 10) + 1;
}
int get_digit(int num, int cnt)
{
if (cnt == 0)
return num % 10;
else
return get_digit(num / 10, cnt - 1);
}
利用同样的办法,可以对所有输入的字符串以ASCII码顺序来排序:
#include <iostream>
#include <vector>
using namespace std;
const int DIGITS = 128; //ASCII码最大值为127
int max_digit(vector<string>); //获得所有字符串中最长的长度
char get_digit(string num, int cnt); //获得从右起第cnt位字符
int main()
{
vector<string> datas = {};
int count;
string str;
cin >> count;
for (int i = 0; i < count; i++)
{
cin >> str;
datas.push_back(str);
}
//对每一位字符倒入、倒出桶
for (int digit = 0; digit < max_digit(datas) + 1; digit++)
{
vector<string> t[DIGITS] = {};
for (auto num : datas)
(t + (int)get_digit(num, digit))->push_back(num);
datas.clear();
for (int i = 0; i < DIGITS; i++)
for (auto num : t[i])
datas.push_back(num);
}
for (auto num : datas)
cout << num << ' ';
return 0;
}
int max_digit(vector<string> datas)
{
int max = 0;
for (auto num : datas)
max = num.length() > max ? num.length() : max;
return max;
}
char get_digit(string num, int cnt)
{
if (cnt > num.length()) //如果访问的位不存在,用ASCII码最小的NULL填补
return NULL;
return num[num.length() - cnt];
}
MSD原理:(待更新)