首先让我们看看BFS是个什么样的运作原理：

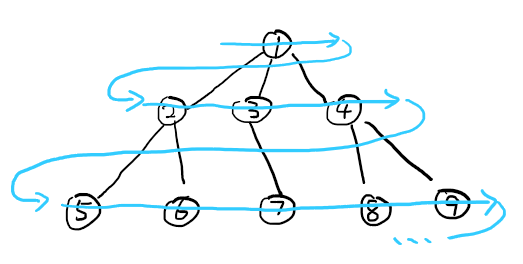
BFS是以广度为优先，也就是先把同级的每一个节点（例如2）先进行运算，同时将和它相邻的需要运算的节点入队，稍后再算（例如2对应的5、6），当同级的所有节点都运算完了的时候（2、3、4），由于队列先进先出的特点，自然轮到了下一级节点（5、6、7、8、9）

然后再看看在BFS中，树是如何剪枝的：

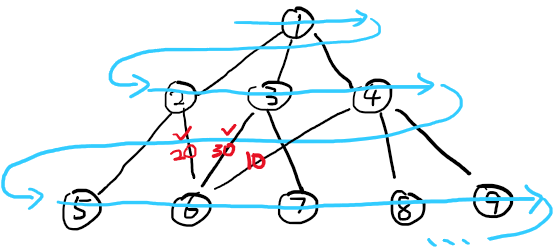
在很多问题中（尤其是棋盘移动之类的），会出现多个节点连上同一个节点的情况（如图中的2、3、4都连着下一级的6），这时候根据条件判断哪一条更优。例如图中红色数值越大越优，当判断到2连6的数字是20时，6的红色值被赋予20，与2相连；当判断到3连6的数字是30时，30比20大，6的红色值被赋予30，与3相连；当判断到4连6的数字是10时，10比30小，6的红色值不变，仍然与3相连；这样，就剪断了2和6,4和6的枝。

那么，没有剪枝的话，会是怎样的呢？

不多解释了，来看一个例子，题目粘下来是这样：

Michael喜欢滑雪，这并不奇怪， 因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子 

 1   2   3  4  5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上，这是最长的一条。

输出最长区域的长度，本例中是 25。

先上代码吧：

#include <iostream>
#include <queue>
using std::queue;
using std::cout;

const int Length = 5;
const int Height[Length][Length] =
{
	{1, 2, 3, 4, 5},
	{16, 17, 18, 19, 6},
	{15, 24, 25, 20, 7},
	{14, 23, 22, 21, 8},
	{13, 12, 11, 10, 9}
};
int maxsteps[Length][Length] = { 0 };

const int direction[4][2] = { {1,0},{0,1},{-1,0},{0,-1} }; //右、下、左、上
//记录每一个点的坐标和从起点到这个点所用的步数
struct point
{
	int x;
	int y;
	int step;
	point(int i, int j, int k):x(i),y(j),step(k) {} //使用初始化列表的构造函数
};
queue<point> pts;
int steps = 0;

void clear(queue<point>& q); //定义一个清空队列的函数
void clear(int arr[Length][Length]); //定义一个清空步数缓存的函数

void bfs(point pt)
{
	cout << "  正在点（" << pt.x << ',' << pt.y << ")\n";
	for (int dir = 0; dir < 4; dir++)
	{
		int next_x = pt.x + direction[dir][0];
		int next_y = pt.y + direction[dir][1];
		if (0 <= next_x && next_x < Length && 0 <= next_y && next_y < Length) //判断方向是否有效
		{
			cout << "    正在测试有效点（" << next_x << ',' << next_y << ")高度\n";
			if (Height[next_x][next_y] < Height[pt.x][pt.y]) //判断下一个方向是否高度更低，能够前进
			{
				if (maxsteps[next_x][next_y] < pt.step + 1) //判断如果向该方向再走一步，是否步数比其他已经尝试的方式都大（也就是砍掉不可能是最大的路径）
				{
					pts.push(point(next_x, next_y, pt.step + 1)); //将下一个可行的点存入队列中
					maxsteps[next_x][next_y] = pt.step + 1; //更新步数表格
				}
			}
		}
	}
	steps = pt.step + 1 > steps ? pt.step + 1 : steps;
	return;
}

int main()
{
	int max_steps = 0;
	for (int start_x = 0; start_x < Length; start_x++)
	{
		for (int start_y = 0; start_y < Length; start_y++)
		{
			cout << "正在以(" << start_x << ',' << start_y << "）为起点\n";
			steps = 0;
			clear(maxsteps);
			clear(pts);
			bfs(point(start_x, start_y, 1));
			while (!pts.empty())
			{
				point next_point = pts.front();
				pts.pop();
				bfs(next_point);
			}
			steps--; //因为最后一次无法前进的点还记了一次步数，所以要减掉
			cout << "步数: " << steps << '\n';
			max_steps = steps > max_steps ? steps : max_steps; //计入最大步数
		}
	}
	cout << max_steps;
	return 0;
}

void clear(queue<point>& q) 
{
	queue<point> empty;
	swap(empty, q);
}

void clear(int arr[Length][Length])
{
	for (int i = 0; i < Length; i++)
	{
		for (int j = 0; j < Length; j++)
		{
			arr[i][j] = 0;
		}
	}
}

首先定义好高度的二维数组，以及用来存到某一点所需步数的临时二维数组；为了代码简洁，同时定义好含四个方向的数组，以及包含着x、y坐标和已经移动的步数的point结构（并且写好构造函数）

主要思路是这样的：

遍历所有的起点
–清空临时数据
–检测起点的可移动信息，并将可以去的下一个点入队（函数bfs()）
–队列非空时，对每个元素再检测可移动信息，并将下一个点入队（函数bfs()）
–计入每个起点最终的最大移动步数

函数bfs的思路：

遍历四个方向的下一个点进行测试
–判断该方向下一个点是否还在二维数组中
—-判断下一个点的高度是否比当前点更小
——判断下一个点是否没有别的路径到达过，或者有但是路径比正在测试的路径短（注意：这里正是树剪枝的办法，直接剪掉不可能是最长的路径）
——–如果均为是，将下一个可以到达的点入队，并且更新步数的表格
遍历完之后，总步数+1（因为最后一次无路可走也会导致步数+1，最终结果要-1）

样例输出：

首先，最终结果输出的是25，也就是从（2,2）点的“25”开始出发的最长路径。

然后以图上的（4,4），既“9”为原点为例，可以看出探索的路径：
最初在起点（4,4），判断到下一个存在的点有（3,4）和（4,3），挑选出没有经过过、并且高度更低的点（3,4），再判断存在的点（4,4），（2,4）和（3,3）。因为高度只能下降，可以没有必要去把曾经经过的点标记为已经过。通过多次测试，最终按照9、8、7、6、5、4、3、2、1的顺序找到了步数为9的最大路径。

以下是完整的输出结果：