
下篇接着上篇的思路,对DFS同样进行剪枝
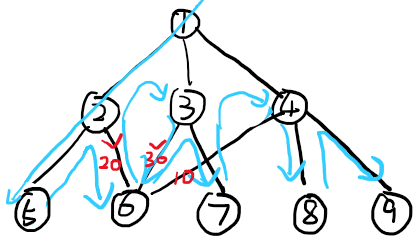
DFS是以深度为优先的搜索方式,先沿着一枝探索到底,然后逐枝从探索过的节点回溯,再探索下一枝。这种情况下,后进先出的栈更适合存储节点信息。同样地,在选取了某个曾经到达过的节点时,判断这枝是否优先度更高,从而保留或者更新枝,达到剪枝的效果。
接着上一段同样滑雪问题的DFS解法代码:
#include <iostream>
#include <stack>
using std::stack;
using std::cout;
const int Length = 5;
const int Height[Length][Length] =
{
{1, 2, 3, 4, 5},
{16, 17, 18, 19, 6},
{15, 24, 25, 20, 7},
{14, 23, 22, 21, 8},
{13, 12, 11, 10, 9}
};
int maxsteps[Length][Length] = { 0 };
const int direction[4][2] = { {1,0},{0,1},{-1,0},{0,-1} }; //右、下、左、上
//记录每一个点的坐标和从起点到这个点所用的步数
struct point
{
int x;
int y;
int step;
point(int i, int j, int k) :x(i), y(j), step(k) {} //使用初始化列表的构造函数
};
stack<point> pts;
int steps = 0;
void clear(stack<point>& q); //定义一个清空队列的函数
void clear(int arr[Length][Length]); //定义一个清空步数缓存的函数
void dfs(point pt)
{
cout << " 正在点(" << pt.x << ',' << pt.y << ")\n";
for (int dir = 0; dir < 4; dir++)
{
int next_x = pt.x + direction[dir][0];
int next_y = pt.y + direction[dir][1];
if (0 <= next_x && next_x < Length && 0 <= next_y && next_y < Length) //判断方向是否有效
{
cout << " 正在测试有效点(" << next_x << ',' << next_y << ")高度\n";
if (Height[next_x][next_y] < Height[pt.x][pt.y]) //判断下一个方向是否高度更低,能够前进
{
if (maxsteps[next_x][next_y] < pt.step + 1) //判断如果向该方向再走一步,是否步数比其他已经尝试的方式都大(也就是砍掉不可能是最大的路径)
{
pts.push(point(next_x, next_y, pt.step + 1)); //将下一个可行的点存入队列中
maxsteps[next_x][next_y] = pt.step + 1; //更新步数表格
}
}
}
}
steps = pt.step + 1 > steps ? pt.step + 1 : steps;
return;
}
int main()
{
int max_steps = 0;
for (int start_x = 0; start_x < Length; start_x++)
{
for (int start_y = 0; start_y < Length; start_y++)
{
cout << "正在以(" << start_x << ',' << start_y << ")为起点\n";
steps = 0;
clear(maxsteps);
clear(pts);
dfs(point(start_x, start_y, 1));
while (!pts.empty())
{
point next_point = pts.top();
pts.pop();
dfs(next_point);
}
steps--; //因为最后一次无法前进的点还记了一次步数,所以要减掉
cout << "步数: " << steps << '\n';
max_steps = steps > max_steps ? steps : max_steps; //计入最大步数
}
}
cout << max_steps;
return 0;
}
void clear(stack<point>& s)
{
stack<point> empty;
swap(empty, s);
}
void clear(int arr[Length][Length])
{
for (int i = 0; i < Length; i++)
{
for (int j = 0; j < Length; j++)
{
arr[i][j] = 0;
}
}
}
几乎没有做改变,仅仅是用栈替换了队列,来存储将要读取的信息。同样,输出的结果依然是25,不过,从中间的步骤可以看出二者的区别。
我们同样以(2,2)为起点,比较一下二者所探索的点的不同之处:
BFS
正在以(2,2)为起点
正在点(2,2)
正在测试有效点(3,2)高度
正在测试有效点(2,3)高度
正在测试有效点(1,2)高度
正在测试有效点(2,1)高度
正在点(3,2)
正在测试有效点(4,2)高度
正在测试有效点(3,3)高度
正在测试有效点(2,2)高度
正在测试有效点(3,1)高度
正在点(2,3)
正在测试有效点(3,3)高度
正在测试有效点(2,4)高度
正在测试有效点(1,3)高度
正在测试有效点(2,2)高度
正在点(1,2)
正在测试有效点(2,2)高度
正在测试有效点(1,3)高度
正在测试有效点(0,2)高度
正在测试有效点(1,1)高度
正在点(2,1)
正在测试有效点(3,1)高度
正在测试有效点(2,2)高度
正在测试有效点(1,1)高度
正在测试有效点(2,0)高度
正在点(4,2)
正在测试有效点(4,3)高度
正在测试有效点(3,2)高度
正在测试有效点(4,1)高度
正在点(3,3)
正在测试有效点(4,3)高度
正在测试有效点(3,4)高度
正在测试有效点(2,3)高度
正在测试有效点(3,2)高度
正在点(2,4)
正在测试有效点(3,4)高度
正在测试有效点(1,4)高度
正在测试有效点(2,3)高度
正在点(1,3)
正在测试有效点(2,3)高度
正在测试有效点(1,4)高度
正在测试有效点(0,3)高度
正在测试有效点(1,2)高度
……
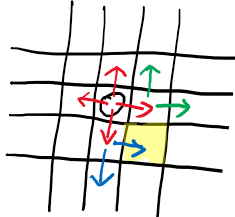
正如图中,程序先按下、右、上、左的顺序发现四个红箭头都可以前往;然后先按下的红箭头到达队列中的第一个点,判断两个蓝箭头均可前往;接着按右的红箭头到达队列中的第二个点,本来绿箭头应该先到达黄色高亮的点,然而已经判断到了蓝箭头已曾到达过这个点了,并且绿箭头到达黄点也并不更优,于是剪断了这根枝,绿箭头只到达了右边和上面的点。
DFS
正在点(2,2)
正在测试有效点(3,2)高度
正在测试有效点(2,3)高度
正在测试有效点(1,2)高度
正在测试有效点(2,1)高度
正在点(2,1)
正在测试有效点(3,1)高度
正在测试有效点(2,2)高度
正在测试有效点(1,1)高度
正在测试有效点(2,0)高度
正在点(2,0)
正在测试有效点(3,0)高度
正在测试有效点(2,1)高度
正在测试有效点(1,0)高度
正在点(3,0)
正在测试有效点(4,0)高度
正在测试有效点(3,1)高度
正在测试有效点(2,0)高度
正在点(4,0)
正在测试有效点(4,1)高度
正在测试有效点(3,0)高度
正在点(4,1)
正在测试有效点(4,2)高度
正在测试有效点(3,1)高度
正在测试有效点(4,0)高度
正在点(4,2)
正在测试有效点(4,3)高度
正在测试有效点(3,2)高度
正在测试有效点(4,1)高度
正在点(4,3)
正在测试有效点(4,4)高度
正在测试有效点(3,3)高度
正在测试有效点(4,2)高度
正在点(4,4)
正在测试有效点(3,4)高度
正在测试有效点(4,3)高度
……
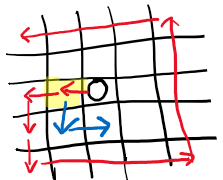
对于DFS,因为栈后进先出,所以按相反的顺序测试点,即左、上、右、下。判断时,点先按第一条路走到底,也就是红箭头一直走到(0,0)处后,再沿着树回溯。跳过一些步骤举例,例如回溯到黄色高亮点往蓝箭头方向搜索时,蓝箭头本来优先探索左方向,然而已经判断到了红箭头已曾到达过这个点了,并且蓝箭头到达这个点也并不更优,于是同样地剪断了这根枝,蓝箭头只能跳过向左,先向右进行搜索。
结论
动态规划利用存储已经运算过的内容,避免了对某些运算内容的重复运算,从而达到了减少运算量的目的。这是一种优化力度大,通用性强的计算机算法、以至数学方法。